Diffusion Rates
Background
What do FTX, Luminar Technologies and BeReal have in common? Wildly different industries, wildly different products yet they had been - quite recently - victims of momentous boom-bust cycles.
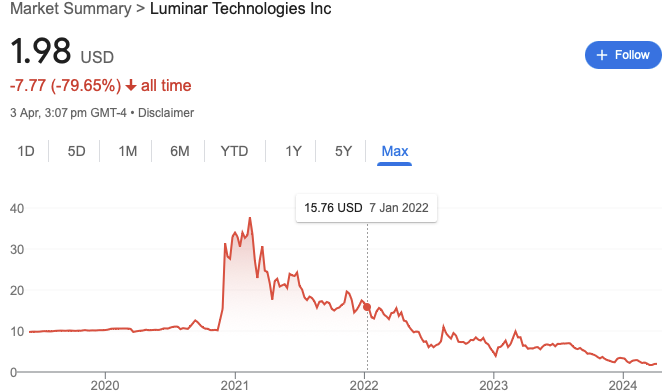
Businesses collapse precipitously due to all sorts of reasons, from securities fraud (Everything is securities fraud!1), to poor financial decisions, making it somewhat less interesting to explore. The companies above basked in the sunshine of serendipity for a brief period of time, and witnessed extraordinarily steep adoption from customers and investors alike. Did they have anyway of knowing they’re going to public darlings? Did the marketing departments cash out on seeing 3 digits in green every day? What would you do if you were to forecast product adoption curves? Just look at how fast apps take over the world currently:
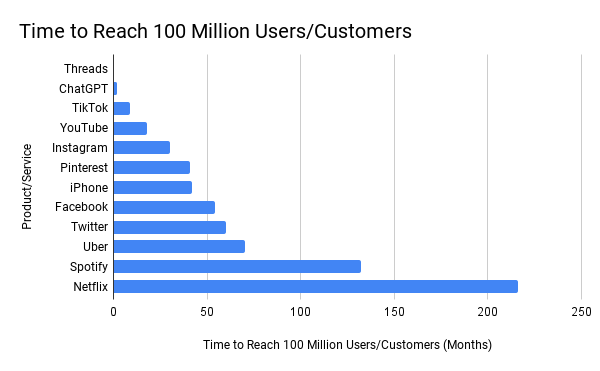
How was it earlier, when things weren’t as “social”? The Bass model attempted to well, model, exactly that. Developed in the 1960s by a marketing professor named Frank Bass, the Bass model allows for a prediction of the purchasers in a period, say annually, as well as the total number of purchasers. So the model helps calibrate the TAM and the rate of growth in getting to TAM.
What’s interesting about the model is, it’s a neat - although lossy - way to capture the essence of the trajectory of a product, both in terms of how revolutionary it was percieved to be at the time of introduction and how quickly people adopted it over time. As a 2000s kid, while I didn’t fully comprehend the scale of progress, I grew up witnessing the evolution of internet in India, from dial-up access to broadband, excitedly speed-testing each new connection and calculating how long downloading a music album will take. That felt like innovation. You didn’t really look at tennis rackets and think about all the engineering breakthroughs that went behind making it back then. And now, after a bit of growing up, I have a deeper appreciation for how indubitably cool a pocket scientific calculator in 1972 would have been. This post seeks to explore Bass model’s framework to better understand the acceleration of technology adoption.
The Bass Model
The Bass model in its basic form is built around three key parameters to predict how new products are adopted in a market:
- Innovation Coefficient (\(p\)): This parameter measures the level of influence the broader market exerts. It’s relevant when an individual’s interest in a product or service is sparked by general media advertising or the novelty of the item, rather than personal recommendations.
- Imitation Coefficient (\(q\)): This captures the effect of social influence or the tendency of people to follow the lead of others in their social circle. It highlights the scenario where someone is drawn to a product because it’s popular among their peers.
- Market Size Estimate (\(m\)): This is used to gauge the potential total number of consumers who will eventually adopt the product, providing an insight into the overall market opportunity for the new product.
The model seems to perform very well for estimating adoption, as illustrated by this HBS case study on satellite radio adoption. While there are limitations, the simplified model remains reasonably robust in providing a solid foundation.
While the Bass model is interesting in its own right and there is a lot more that can be said, I wanted to take a closer look at the rate at which technologies are diffusing and whether it’s speeding up. To what degree are \(p\) and \(q\) contributing to the speed up?
We have a variety of sources suggesting that the rate of diffusion of technology has sped up in the recent past.
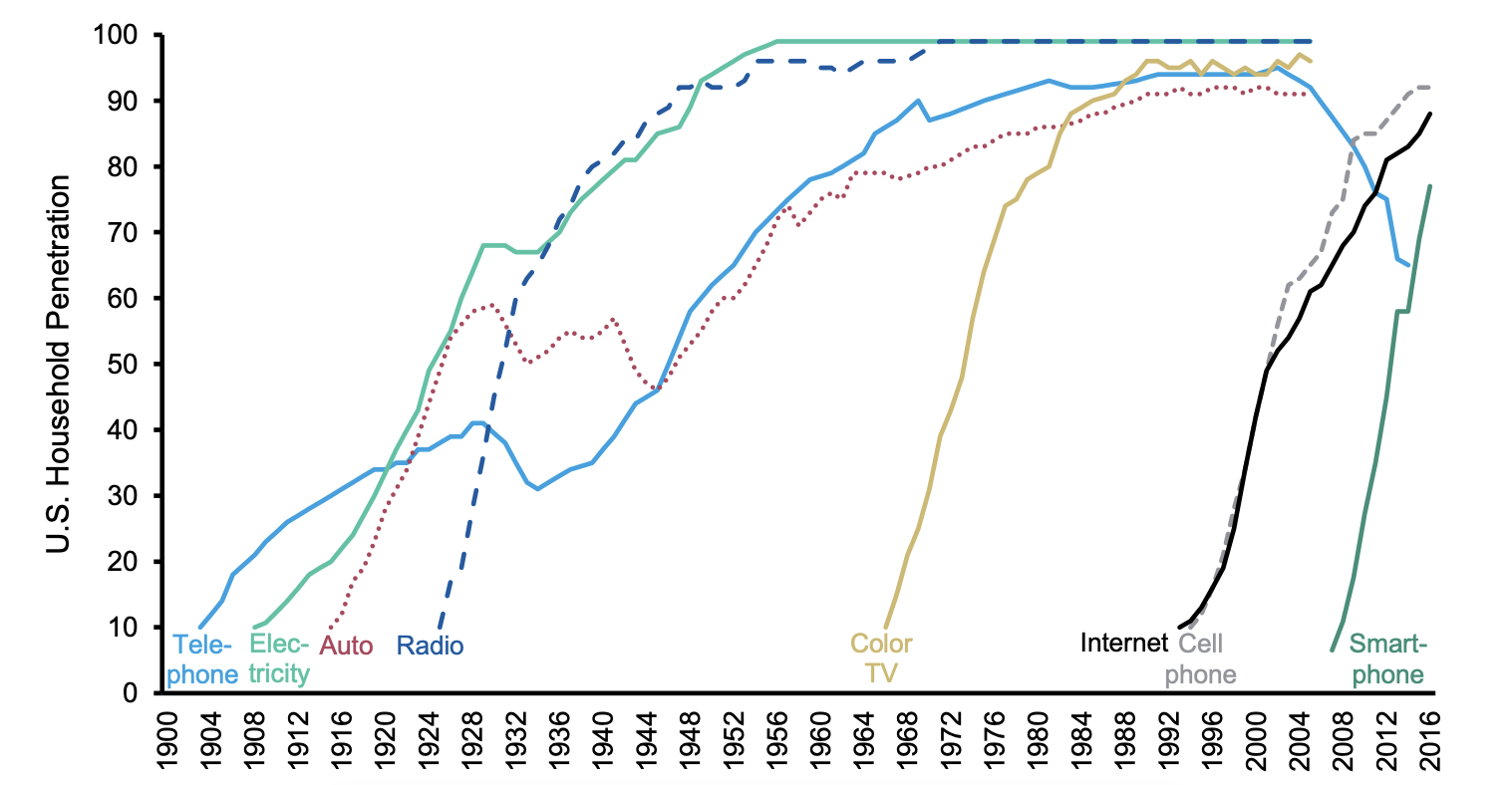Source: Morgan Stanley, Asymco
The evolution of coefficients
The recent sharp increase in adoption curves prompts a practical examination of the roles of innovation (\(p\)) and imitation (\(q\)) coefficients. In today’s digital age, the influence of \(q\) has likely grown due to the rapid spread of information and ideas through social media and other online platforms, leading to faster and wider product adoption. This suggests a significant increase in \(q\)’s value across various industries. On the other hand, the frequency of true innovations (\(p\)) making it to market may not have increased at the same rate. However, when innovations do emerge, their reach and impact are quickly amplified through digital means. The narrative is no longer just about the product but how it’s woven into the fabric of society by the threads of innovation and imitation.
To get a feel for how market adoption curved change with parameters, play around with the model below! Notice how changing market size doesn’t really change the steepness of the curve, only \(p\) and \(q\) do. Properties of the market, such as its size, whether it’s saturated or not, existing competition, affect the number of people a product would eventually reach and it does affect \(p\) and \(q\) in subtler ways, but in a sandbox environment you could tinker with each individually and come to the conclusion that if steepness is all that matters, \(p\) and \(q\) are what the marketing department at your firm should be concerned with. Today’s adoption curves result in S-shaped tetris blocks building the future - just look at what the smartphone curve looks like and think about what the ChatGPT curve might look like!
S-shape, or the reverse squiggly
Playground
How did this interplay pan out before social media existed? In its place, TV, Radio, and Newspapers gave new avenues of product distribution. More adoption of TV increased the adoption of products that were marketed through the telemarketing channels. It’s self-evident that besides the primary benefits offered by new technologies, they have ripple effects throughout the economy which leads to faster adoption of other technologies.
Let’s load the dataset first and take a look at how it’s structured. For context, the dataset has Bass model parameters for 54 products - modest in size - introduced through the 20th century.
| Vertical | Product/Technology | Period of Analysis | Period of Analysis Start Year | Period of Analysis End Year | p | q | m |
|---|---|---|---|---|---|---|---|
| Agricultural | Tractors (thousands of units) | 1921-1964 | 1921 | 1964 | 0.000 | 0.134 | 5201.0 |
| Agricultural | Hybrid corn | 1927-1941 | 1927 | 1941 | 0.000 | 0.797 | 100.0 |
| Agricultural | Artificial insemination | 1943-1959 | 1943 | 1959 | 0.028 | 0.307 | 73.2 |
| Agricultural | Bale hay | 1943-1959 | 1943 | 1959 | 0.013 | 0.455 | 92.2 |
| Medical Equipment | Ultrasound imaging | 1965-1978 | 1965 | 1978 | 0.000 | 0.534 | 85.8 |
The dataset looks good to go, now let’s try see if \(p\) and \(q\) are correlated with the year the product was introduced in the market (for the sake of this post, I’m assuming the analysis start year as the year the product was introduced).
| Parameter | Correlation with Start Year | P-value |
|---|---|---|
| p | 0.293513 | 0.031233 |
| q | 0.318733 | 0.018823 |
Both \(p\) and \(q\) are slightly positively correlated with product introduction years, with p<0.05, implying a statistically significant correlation. While we could have expected this of \(q\), it’s interesting to observe that \(p\) has followed the same trend. As time passed, products have gotten more and more innovative, so you could make the case that prior technology serves as a foundation for more creative breakthroughs - a great example of this is the humble transformer birthing shoggoth within half a decade.
We went from lawful good to chaotic evil really fast
Historical and Modern Adoption Rates
The correlation holds for newer technologies introduced in the market, as exemplified by this chart compiled by OurWorldInData. We’re in the era of competing how close to 90 degrees our user adoption curves are.
You can eyeball through the graphs and notice how much more steeper the curves for recent technology looks like compared to older ones. Product adoption levels is now measured in months rather than years.
Plotting products
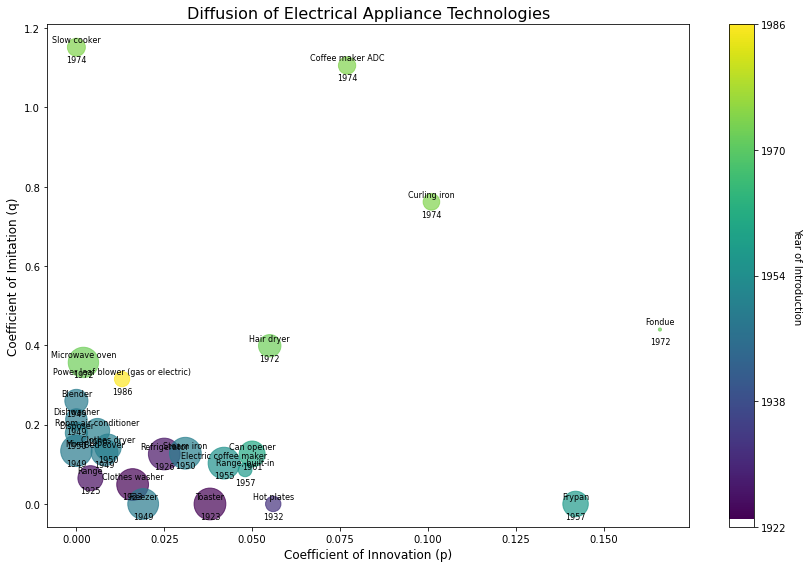
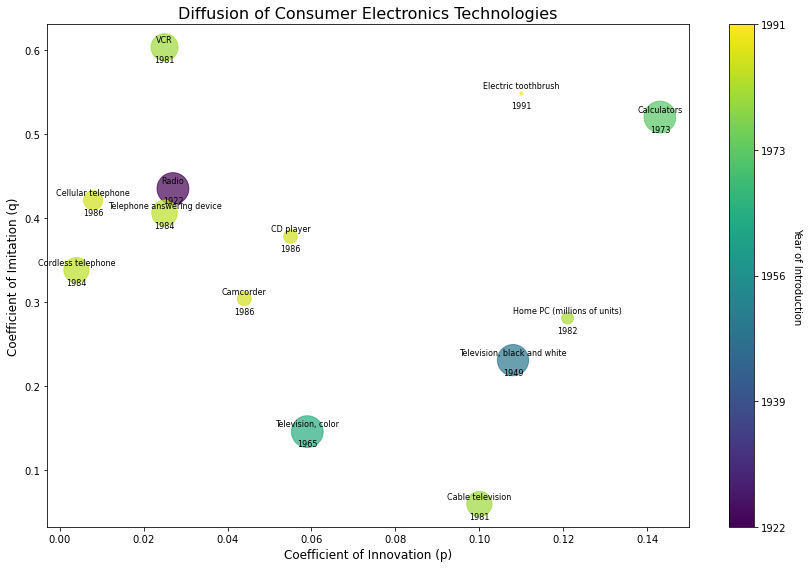
Some thoughts
- Did people not think dishwashers and microwaves as revolutionary? It’s odd that a bunch of electrical appliances are bunched together on the lower left part of the graph. I understand a low y-axis value, but the x-values are throwing me off. Maybe the pre-1950s era just a harder time to sell products in? Few hypotheses I can think of is stifled economic growth due to the World Wars, mass paranoia, general lack of interest, low S&M budgets. Could be a multitude of things, possibly all at once, but hard to believe that the products weren’t perceived as innovative.
- It’s interesting that the electric toothbrush introduced in 1991 was more innovative than a color TV launched in 1965. I suspect there’s an interesting story here, maybe similar to the blue LED.
- Although the dataset isn’t that big, there’s a visible trend towards \(p\) increasing over time, which is somewhat counter-intuitive to me. Maybe I follow doomer-leaning accounts on X, but the narrative I’ve usually come across is innovation has been harder and harder to find.
- Calculators securing the top right position is a fun piece of information. Maybe it was because of the size? The HP-35, the world’s first scientific pocket calculator, was designed the way it was to fit into William Hewlett’s shirt pocket. Sounds like another interesting rabbit hole.
Having been around for a long time, the Bass model has been researched extensively, with academics making numerous modifications to enhance the application and accuracy of the model, but it suffers from serious limitations that prevents it from being a silver bullet. In the current context, the biggest problem is that product life cycles have shrunk over the years, and new technologies cannibalize or supersede the old at a faster pace, reducing the validity of the Bass forecast. Other issues include the constancy of the parameters over time, requirement for sales data over a few years for accurate estimation and calibration of the probability of failure. As far as I’m aware, this is just one of the many other methods used to forecast sales, and doesn’t really command all that much priority these days. Still pretty cool that with three numbers you can glipmse into the number of adopters with sufficiently high accuracy.